评价指标--metrics

一个非常好的关于机器学习算法中常用评价指标的github项目 Metrics，该项目作者 Ben Hamner 是 Kaggle 组织的联合创始人及 CTO。

Confusion matrix

在机器学习领域，混淆矩阵用来衡量分类模型在测试数据上的表现。矩阵的列表示模型预测的类别实例，而行表示真实的类别实例。 下图中是分类模型 对猫、狗、兔子三种动物进行分类的结果：

图中第一行，模型将8只猫分对了5只，分错了3只（错分成狗）；第二行中，模型将6只狗分对了3只，分错了3只（其中2只错分成了猫，1只错分成了兔子）； 第三行中，模型将13只兔子分对了11只，分错了2只（错分成了狗）。可以看出该模型容易混淆猫和狗两种动物，而对兔子的识别较为准确。

因此，通过混淆矩阵不仅仅可以计算出模型在每一类别上的正确率，还可以得到错误分类的具体情况，这在数据类别严重不均衡的情况下尤为重要了。比如数据集中如果有95只猫，2只狗， 3只兔子， 那么当分类模型把所有输入都判断为猫的情况下，分类准确率仍达到95%；但是通过混淆矩阵我们除了可以得出综合准确率为95%以外，还可以得出模型判别猫的准确率为100%，判别狗和兔子的准确率却为0%。

我们以二分类问题为例来介绍一些更为专业的术语。

图中：

condition positive – 阳性样本的真实数目 (c+d)

condition negative – 阴性样本的真实数目 (a+b)

predicted condition positive – 模型预测结果中阳性样本的数目 (b+d)

predicted condition negative – 模型预测结果中阴性样本的数目 (a+c)

true positive (TP) – 实际为阳性样本且判断为阳性的数目 (d)

true negative (TN) – 实际为阴性样本且判断为阴性的数目 (a)

false positive (FP) – 实际为阴性样本但判断为阳性的数目 （b, Type I error: 错把未发生的事件判断为发生）

false negative (FN) – 实际为阳性样本但判断为阴性的数目 (c, Type II error: 把已发生的事件遗漏了)

• accuracy (ACC):

  准确率：ACC = $\frac{a+d}{a+b+c+d}$

• sensitivity, recall, hit rate, true positive rate (TPR):

  在真实阳性样本中，预测正确的样本所占的比例： TPR = $\frac{d}{c+d}$

• precision, positive predictive value (PPV):

  预测结果为阳性的样本中，预测正确的样本所占比例： PPV = $\frac{d}{b+d}$

• specificity, true negative rate (TNR):

  在真实阴性样本中，预测正确的样本所占的比例： TNR = $\frac{a}{a+b}$

• negative predictive value (NPV):

  预测结果为阴性的样本中，预测正确的样本所占比例： NPV = $\frac{a}{a+c}$

F1 score (wiki)

F1 score 是综合考虑了 precision 和 recall 的指标，用来衡量分类模型的准确率

$$F1 = 2 \cdot \frac{1}{\frac{1}{recall}+\frac{1}{precision}} = \frac{2d}{2d+b+c}$$

F1 的值在区间 [0, 1] 内，且越靠近 1 表明模型的准确率越高。

另外一种称为 $F_\beta$ 形式如下:

$$F_\beta = (1+\beta^2) \frac{1}{\frac{\beta^2}{recall}+\frac{1}{precision}}=\frac{(1+\beta^2)d}{(1+\beta^2)d+\beta^2c+b}$$

可以看出 $\beta^2$ 的值越大，$F_\beta$ 赋予 recall 的权重就越大，也就是说 $F_\beta$ 的值更多的体现了 recall 的值。

ROC (receiver operating characteristic) curve

An introduction to ROC analysis

同 confusion matrix 一样, ROC 曲线用来衡量分类模型的优劣。如下图所示， x 轴表示 false positive rate (1-specificity)， y 轴表示 true positive rate (sensitivity)，因为 ROC 包含了 sensitivity 和 specificity， 因此 ROC 曲线上的每一点包含了该点对应的 confusion matrix 中的所有信息。

这里解释一下 x 轴和 y 轴的来历，ROC 是在二战时期提出，用来探测敌军雷达信号wiki， 其中 y 轴表示对于值为 “1”（危险） 的信号，探测器将其正确判断为“1”的概率； x 轴表示对于值为“0” （安全）的信号，探测器将其错判为“1”的概率，即假警报(false alarm)。 使用这两个值来衡量探测器的性能。

模型表现越好，其对应的 (FP, TP) 点越靠近图中的左上角 (0, 1); 反之则越靠近图中的右下角 (1, 0)。图中的对角线 (红色虚线) 表示 模型在两个类别上的预测准确率均为 50%

我们以下面的代码来计算 ROC

def binary_roc_curve(y_true, y_pred, pos_label=1, sample_weight=None):
    '''
    for details, refer to 
    https://github.com/scikit-learn/scikit-learn/blob/14031f6/sklearn/metrics/ranking.py#L187

    inputs
    -------
    y_true: 1D array, shape=[n]
        True targets of binary classification
    
    y_pred: 1D array, shape=[n]
        Estimated probabilities of binary classification
    
    pos_label: int, the label of positive class

    sample_weight: array-like of shape=[n]

    '''
    classes = np.unique(y_true)
    if sample_weight is None:
        sample_weight = np.ones_like(y_true, dtype=np.float)

    # y_true = np.array([0, 0, 1, 1, 0]), 
    # y_pred = np.array([0.1, 0.4, 0.35, 0.8, 0.1])
    y_true = (y_true == pos_label)
    
    desc_idx = np.argsort(y_pred)[::-1]
    y_true = y_true[desc_idx] # [True, False, True, False, False]
    y_pred = y_pred[desc_idx] # [0.8, 0.4, 0.35, 0.1, 0.1]
    sample_weight = sample_weight[desc_idx]

    distinct_value_idx = np.where(np.diff(y_pred))[0] #[0, 1, 2]
    threshold_idx = np.r_[distinct_value_idx, y_true.size - 1] # [0, 1, 2, 4]

    tps = np.cumsum(y_true * sample_weight)[threshold_idx] # [1, 1, 2, 2]
    fps = np.cumsum(sample_weight)[threshold_idx] - tps # [0, 1, 1, 3]
    tpr = tps / tps[-1] # [0.5, 0.5, 1., 1.]
    fpr = fps / fps[-1] # [0., 0.333, 0.333, 1.]
    threshold = y_pred[threshold_idx] # [0.8, 0.4, 0.3, 0.1]

    return fpr, tpr, threshold

名字的由来：ROC 分析来源于信号探测理论，该理论发展于二战时期，主要用来分析雷达图像。雷达接收机操作员 (radar receiver operator) 需要对雷达图像上的闪光点进行判断，判断其是否为敌军目标。 操作员便是基于信号探测理论对雷达图像进行分类，因此称该方法为 Receiver Operating Characteristic。直到 1970’s 年，ROC 方法才广泛的用于分析医疗测试结果。

AUC

动态的画出二分类问题的 ROC 曲线

Kaggle url2

def auc(x, y, reorder=False)
    '''
    for details, refer to 
    https://github.com/scikit-learn/scikit-learn/blob/14031f6/sklearn/metrics/ranking.py#L187

    inputs
    ------
    x: 1D array, shape=[n], fpr
    y: 1D array, shape=[n], tpr
    reorder: boolean, optional (default=False)

    return
    ------
    auc value: float
    '''
    if reorder:
        order = np.lexsort((y, x))
        x, y = x[order], y[order]
    
    area = np.trapz(y, x)
    return area

皮尔逊相关系数 Pearon correlation

$$r_{xy} = \frac{\sum_i(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_i (x_i - \bar{x})^2 \sum_i (y_i - \bar{y})^2}} =\frac{n\sum_i x_i y_i - \sum_i x_i \sum_i y_i}{\sqrt{n\sum_i x_i^2 - (\sum_i x_i)^2} \sqrt{n\sum_i y_i^2 - (\sum_i y_i)^2}}$$

通常 pearson 系数的报告形式为：

r(df) = pearson-correlation, p-value = statistical significance，其中 df = N - 2

def correlation_pearson(y_pred, y_true):
    """
    return:
        pearson correlation coefficient
    """
    cov = np.mean(y_pred * y_true) - np.mean(y_pred) * np.mean(y_true)    
    y_pred_std = np.std(y_pred)
    y_true_std = np.std(y_true)

    corr_pearson = cov / (y_pred_std * y_true_std)

    return corr_pearson

此系数用来计算两个变量的线性相关性，包括方向 (正相关或负相关) 和强度 (介于[0, 1]之间，0表示非线性相关，1表示完全线性相关)。如果已知两个变量之间是非线性关系，比如指数关系， 那么计算出来的 Pearson 系数值没有意义。在两个变量满足线性关系的前提下，可以通过画出他们的散点图来确定线性关系是否成立，pearson 系数反应了该线性关系的程度，但 Pearson 方法本身并不能判断此线性关系是否成立。定量地，Pearson 方法会穿过所有数据点画出一条最佳的拟合直线，并给出此直线在多大程度上符合该数据集。

要求：

1. 两个变量必须是连续变量 types-of-variables。
2. 两个变量必须近似满足正态分布。(Pearson 方法为参数化统计方法 wiki)
3. 两个变量必须满足线性关系。
4. 数据中异常值应尽可能的少。
5. 两个变量应具有同方差 homoscedasticity

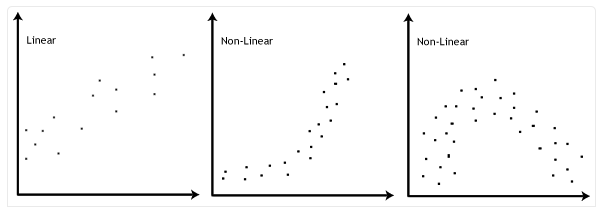
通过两个变量之间的散点图的形状决定线性关系的前提是否满足，第一幅图满足线性关系，第二三幅图不满足。

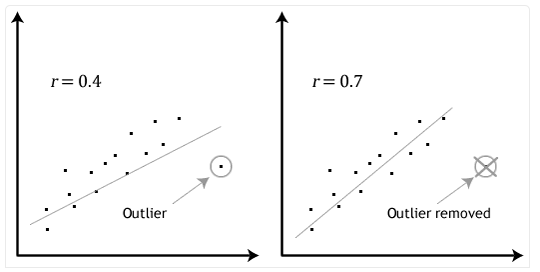
Pearson 系数对异常值会很敏感，少量的异常值就会导致系数值的巨大变化。确定异常值的简单方法便是通过画出两个变量的散点图来确定，如图中所示。

Homoscedasticity 是指落在直线 x=x_0 （垂直线）上的数据点的方差，随着 x_0 的移动保持一致；反之落在 y=y_0 （水平线）上的数据点的方差，随着 y_0 的移动保持一致。

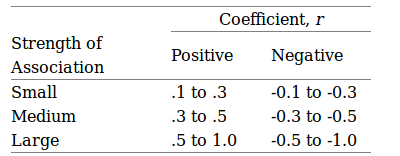
具体系数值达到多少才算相关性比较强，并没有 统一的规定，下图可以用来作为参考，但实际应用过程中还是需要根据所用数据进行调整

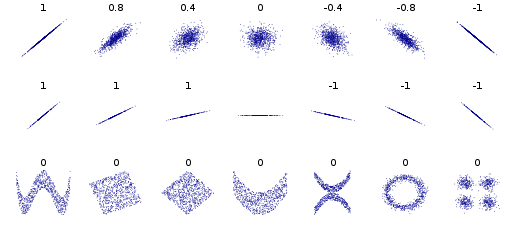
wiki 图中展示了若干数据集 (x, y), 以及各自的 pearson 相关系数的值。图中第一行通过pearson系数反应了数据集中变量x 和 y 之间的相关性（方向和强度）；图中中间行表明 pearson 系数 与数据拟合直线的斜率无关，中间的数据集没有计算出 pearson 系数是因为变量 y 的方差为0；图中第三行表明 pearson 系数并不适用于 非线性数据集。

斯皮尔曼等级相关系数 Spearman’s rank-order correlation

Spearman 等级相关系数 (以下简称 spearman 系数) 用来计算两个顺序类型变量之间的单调相关性，包括方向 (正相关或负相关) 和强度 (介于[0, 1]之间，0表示无单调相关，1表示完全单调相关)。 这种单调性是指随着一个变量观测值的增加，另外一个变量的观测值也相应的增加，或者相应的减小，而增加/减小的幅度对计算结果无影响。

如果两个变量 X, Y 是连续型变量，需要先计算出各自观测值 x_i 和 y_i 的排序下标 rankx_i 和 ranky_i，并使用该下标计算 spearman 系数。计算排序下标的 python 代码如下：

def correlation_pearson(y_pred, y_true):
    """
    refer https://statistics.laerd.com/statistical-guides/spearmans-rank-order-correlation-statistical-guide.php 
    for details about ranking tied data
	
    inputs
	x: list of num or 1D np.ndarray
    return:
	tied_rank of x: list of num
    """

    total_num = len(x)
    x_sorted = [[e, r] for e, r in zip(sorted(x), range(total_num))]

    start_e = x_sorted[0][0]
    start_rank = 0
    for e, r in x_sorted:
        if e == start_e:
            pass

        else:
            mean_rank = np.mean(np.asarray(range(start_rank, r)))
            for idx in range(start_rank, r):
                x_sorted[idx][1] = mean_rank
            start_rank = r
            start_e = e
		
    mean_rank = np.mean(np.asarray(range(start_rank, total_num)))
	
    for idx in range(start_rank, total_num):
        x_sorted[idx][1] = mean_rank

    x_sorted_dict = dict(x_r for x_r in x_sorted)

    return [x_sorted_dict[e]+1 for e in x]

下图是某班级学生的 English 和 Maths 成绩，我们将 English 和 Maths 看做变量，则下图即为该变量的观测数据。

为了计算变量的 spearman 系数，我们使用上面的代码计算出变量的排序下标，如下图所示：

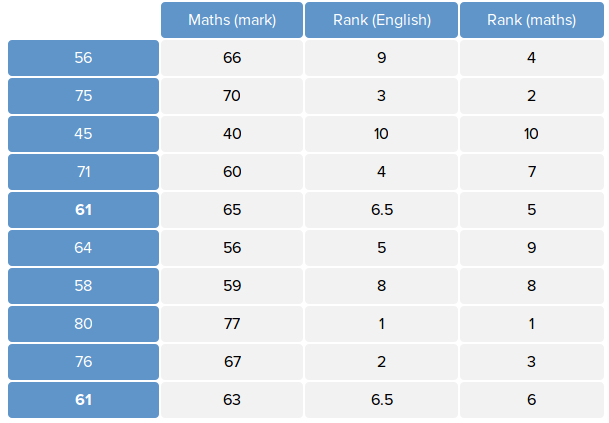
则计算 spearman 系数的公式如下:

$$\rho = \frac{\sum_i (x_i - \bar x)(y_i-\bar y)}{\sqrt{\sum_i(x_i - \bar x)^2 \cdot \sum_i(y_i - \bar y)^2}}$$

这里 (x, y) 表示 (rank_English, rank_Maths)。如果变量 x, y 的各自的观测数据中均不存在相同的值，也就是不存在 tied rank 时，可以 使用下面更为简介的公式计算：

$$\rho = 1 - \frac{6\sum_i d_i^2}{n(n^2 - 1)}$$

其中 d_i = x_i - y_i。

要求：

1. 两个变量必须是顺序类型，或者连续类型 [types-of-variables]。

2. 两个变量之间必须满足单调性 (此处单调性的限制性条件要比线性弱，因此当数据集由于不满足线性条件而不能使用 pearson 系数时，可以考虑使用 spearman 系数)。

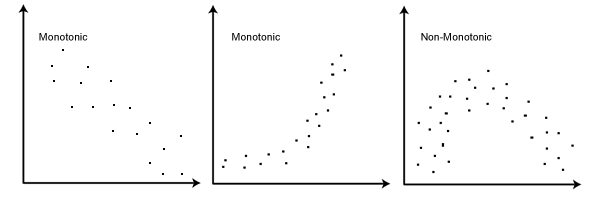
特点：

1. 对于不满足正态分布的变量，spearman 系数同样适用。
2. spearman 系数对异常值并不敏感，即异常值并不会使计算出的值的不可靠。

---

参考：