损失函数

定义

对于分类问题，假设我们有数据集 $D=\{(\vec x_1, \vec y_1), (\vec x_2, \vec y_2), ..., (\vec x_N, \vec y_N)\}$，以及模型 $F$，其中 $\vec x_n,\: \vec y_n$ 均为向量，$\vec y_i$ 满足 one-hot 形式； 为了量化模型在数据集$D$上的表现能力，也就是模型输出结果与真实结果的吻合度，我们通过定义损失函数 (loss function) 来计算该值。 假设模型的输出为 $\vec f = F(\vec x)$，我们有如下两种损失函数：

• 平方和误差 (sum squared error)

$$L = \frac{1}{N}\sum_{n=1}^N ||\vec y_n - \vec f_n||^2$$

可以看出上式中使用向量 $\vec y$ 和 $\vec f$ 的欧式距离来衡量模型表现能力，如果 $\vec f_n$ 越接近目标向量 $\vec y_n$ （$\vec f \rightarrow \vec y$），那么损失函数 $L$ 的值越小，反之越大。因此可以通过最小化 $L$ 来提高模型的表现能力。

• 交叉熵 (cross entropy)

$$L = －\frac{1}{N}\sum_{n=1}^N \sum_{i} y_n^i ln\: f_n^i$$

因为向量 $\vec y_n$ 是 one-hot 形式，因此向量中的元素值 $y_n^i\in \{0, 1\}$；而向量 $\vec f_n$ 中的元素值 $f_n^i\in [0, 1]$。那么当

　1. $y_n^i = 0$ 时，　

　上式中等式右侧第一项 $y_n^i\: ln \:f_n^i = 0$， 第二项 $(1-y_n^i)\: ln\: (1 - f_n^i)＝ln\: (1 - f_n^i)$

　的值随着 $f_n^i \rightarrow 0$ 也不断接近 $0$。

　２. $y_n^i = １$ 时，　

　上式中等式右侧第一项 $y_n^i\: ln \:f_n^i = ln\: f_n^i$ 的值随着 $f_n^i \rightarrow 1$ 不断接近 $0$；

　第二项 $(1-y_n^i)\: ln\: (1 - f_n^i)＝0$。

因此交叉熵形式的损失函数在 $\vec f \rightarrow \vec y$ 的过程中不断接近 0，同平方和误差一样可以用来衡量模型在数据集上的表现能力，并且等式右侧的负号保证 $L\ge 0$。

为了更直观的理解使用交叉熵来量化模型输出结果与真实结果的吻合度，我们看下面的例子：

例子

现在我们考虑二分类问题 (类别 $c_0$ 和 $c_1$) 的交叉熵。这时向量 $\vec y$ 是二维向量， $\vec y[0]$ 和 $\vec y[1]$ 分别表示 $\vec x$ 属于 $c_0$ 和 $c_1$ 的概率。为了简化问题，我们假设数据集 $D$ 中只包含 $c_0$ 类别的样本，这时:

$$y_n[0] \equiv 1, \quad y_n[1]\equiv 0 \qquad n=1, 2, ..., N$$

另外，我们在区间 $[0,\: 1]$ 上进行 beta 分布随机采样来代表样本属于 $c_0$ 类别的概率。

下图展示了 beta 分布函数中的参数 $(a, b)$ 在取不同值的情况下函数的曲线图，可以看出在固定 $b$ 的条件下，随着 $a$ 值不断增加，曲线不断向右偏斜，即采样数据的值有更大的概率偏向 1。我们已知将样本数据 $\vec x$ 输入模型 $F$ 后，模型将会输出两个概率值 $f[0]$ 和 $f[1]$，他们分别代表 $\vec x$ 属于 $c_0$ 和 $c_1$ 的概率， 如果我们将采样得到的值作为 $f[0]$，相应的 $f[1] = 1 - f[0]$，那么随着 $a$ 值的不断增大，采样的值有更大的概率接近真实的值，即 $f[0] \rightarrow y[0]$， $f[1] \rightarrow y[1]$， 因此相应的交叉熵 $L$ 的值将不断减小。

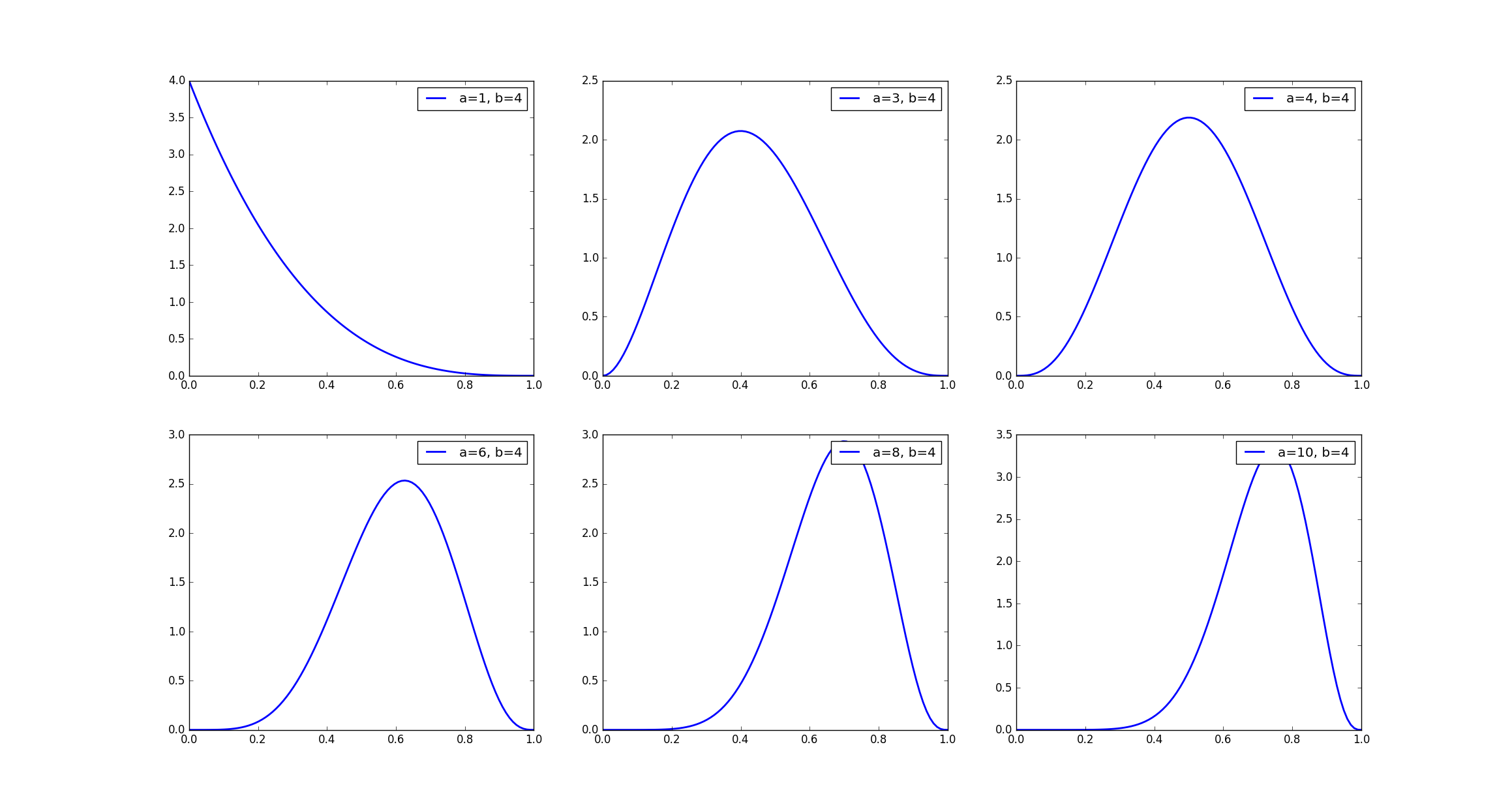
生成数据的代码如下：

def gen_data(N, a, b):
  """
  N: 数据集中的样本数量
  a, b: beta 分布中的参数
  """
  #　样本的真实标签数据
  y = np.zeros(shape=(N, 2))
  y[:, 0] = 1.

  #　模型预测出的概率值
  f_0 = np.random.beta(a, b, size=(N, 1))
  f_1 = 1. - f_0
  f = np.hstack([f_0, f_1])
  return f, y

下图显示了交叉熵 $L$ 与参数 $a$ 之间的曲线图， $N$ 取值 10e4。

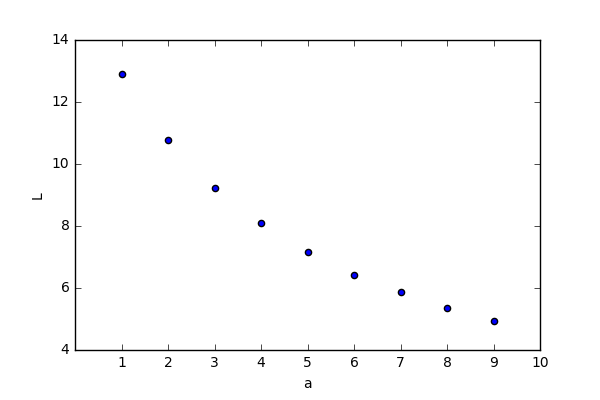
可以看出随着 f 不断的接近 y ($a$ 的不断增大)，$L$ 的值不断下降。

交叉熵与信息论 (information theory)

信息传递的过程涉及 编码 (encoding) 和 解码 (decoding) 两个步骤，编码 是将单词转换成二进制数字 (比如 dog$\rightarrow$ 01011)，解码是将二进制数字反编码为相应的单词 (01011$\rightarrow$ dog)。

根据信息论，最优编码长度 $L(w) = log_2(\frac{1}{p(w)})$ (详细介绍参考博客)， 其中 $w$ 表示词汇表中的单词， $p(w)$ 表示单词 $w$ 在通信过程中的使用概率 (通过统计得到)。 那么在概率分布 $p$ 下，单词的平均编码长度为：

$$H(p) = \sum_w p(w) log_2 (\frac{1}{p(w)}) = - \sum_w p(w) log_2 \:p(w)$$

在通信过程中，我们最终的目的是要把需要表达的意思准确无误的传递过去，避免模棱两可的信息。比如前线需要把战事的结果 (胜利或者失败) 传递给后方，如果使用 $0$ 和 $1$ 分别表示这两种结果的话，我们仅需要 1 bit 长度的编码方式就可以清楚无误的将信息传递过去；如果当前战事并没有分出胜负，处于胶着状态，但可以判断出哪一方处于优势，哪一方处于劣势；这时需要传递的信息可能情况增加到了四个 (胜利，失败，胶着，我方占优势，和 胶着，敌方占优势)，我们至少需要 2 bit (00, 01, 10, 11 分别表示四种状态) 长度的编码才使得信息的接收方明白当前的战事情况。对于发送邮件这样更为普遍的情况，我们 需要表达的意思 并不是一个单词可以表示的，会涉及更多的因素，比如委婉的回绝，礼貌的问候而不包含其他具体的事情等等。假设现在我们手上有一份日常用语词汇表 (比如1000个常用汉字)，我们需要从这份词汇表中挑选出合适的单词，并组合出能够表达我们意思的一封邮件来。对于那些从事 编码-解码 的技术人员来说，如何设计一份编码-解码对照表才能使得每天发送的海量邮件的编码总长度最小？上式中的熵 $H(p)$ 便是解决此问题的最优办法，即通过统计出每个词汇在发送邮件过程中的使用概率分布 $p(w)$，便设计出一套 编码-解码 对照表，使得词汇的平均编码长度最短。

但是上面介绍的 编码-解码 规则是针对于发送邮件这一特定问题而设计的，对于打电话这一问题，由于电话中人们使用各个词汇的概率 $q(w)$ 与发邮件 $p(w)$ 有很大差别，因此如果仍然使用该 编码-解码 对照表的话，会使得词汇平均编码长度：

$$H_p(q) = - \sum_w q(w) log_2 \:p(w)$$

远远大于 $H(p)$，而 $H_p(q)$ 便是交叉熵的形式。这里我们引入 Kullback-Leibler divergence (KL 散度)，其定义为

$$KL_p(q) = H_p(q) - H(p)$$

KL 散度可以用来衡量两种分布之间的”距离”，当两种分布无限接近时，KL 散度的值趋向于 0。

• Binary-cross-entropy

当分类的类标签彼此独立，不满足互斥时， $\vec y_n$ 不再时 one-hot 类型，即其中的任意分量 $y_n^i \in [0, 1]$，比如一张图片中可以包含 cat, dog, elephant 三种动物，此时 $\vec y_n = [1, 1, 1]$， 而模型预测结果可能是 $\vec f_n = [0.2, 0.7, 0.6]$， 此时使用交叉熵可有如下形式

$$L = －\frac{1}{N}\sum_{n=1}^N \sum_{i} y_n^i ln\: f_n^i + (1 - y_n^i) ln\: (1 - f_n^i)$$ $$minimize \: L(\vec W, \vec b)$$ $$\frac{\partial L}{\partial W_i} \quad \frac{\partial L}{\partial b_i}$$

(ref to func tensorflow.nn.sigmoid_cross_entropy_with_logits)