联合分布
联合分布
-
分别为
连续和离散的情况如下图所示黄色线和绿色线分别表示联合概率函数 和
其中为连续变量, 为离散变量
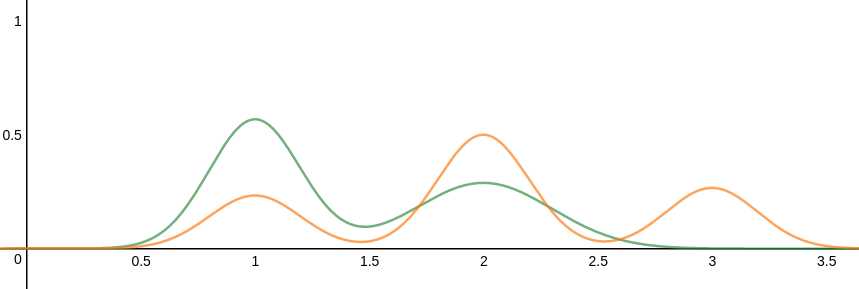
在已知 和 的前提下,我们来计算边缘概率(marginal probability) 和 。
-
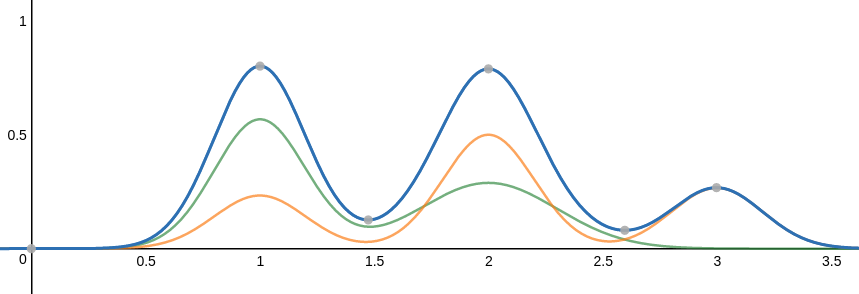
边缘概率可以通过
计算出来,即两条联合分布曲线的叠加,如下图中的蓝色线所示,且满足 。
-
因为是离散变量,因此我们可以方便的计算出
也就是说红色线与 轴之间的面积表示概率,蓝色线与 之间的面积表示概率 ,并且有
假如是模型的输入, 是模型的输出,那么模型将如何对轴进行区间划分以使得分类的准确率达到最高,也就是最大化下面的函数 [PRML]
其中 表示轴上的第分类区间,表示数据集的联合分布。我们该如何理解上式所代表的意义呢?想象我们在高维空间划分出来很多小的子区域,这些子区域都是由多个超平面包围起来构成的,并且每个子区域都有自己所属的类别(属于类别的子区域可能有多个,并且互相不链接,因此我们写作表示类别的第子区域,并且),这时当有新的数据点恰好落在子区域,那么我们希望数据点属于类别的概率大于其他类别的概率,即
这也就是上面最大化的意义。
在下图中我们标记出来三个点(黄色曲线和绿色曲线的交叉点),这三个点便是我们寻找的划分点。由它们划分出的四个区间,
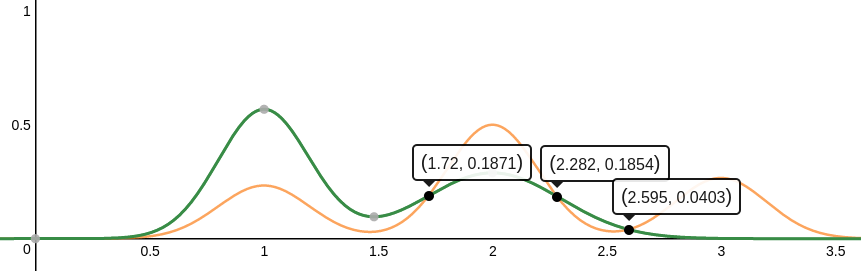
这里我们直接得出当
时,方程得以最大化(参考上一段的解释)。 因此,如果我们构建的学习模型能够划分出等式进行分类,那么该模型便具有最高的分类正确率。然而实际问题中我们通常得不到变量的联合分布函数(),如图中的黄色和绿色曲线。我们将证明通过乘法公式
最大化公式 等价于
其中 表示在已知 的信息条件下, 的条件概率,此条件概率便是各种学习模型的输出结果,因此是可以得到的。
-