翻译－神经网络，流形和拓扑

A chinese version of blog Neural Networks, Manifolds, and Topology (by Christopher Olah)

以下内容直接翻译自博客 Neural Networks, Manifolds, and Topology (作者 Christopher Olah)

近来，深度神经网络引起人们极大的热情和兴趣，这源于深度神经网络模型在计算机视觉领域所取得的突破。

然而，对于这些模型仍有很多未解决的问题。其中一个便是我们仍不能完全理解神经网络模型的工作原理。比如，当我们把模型训练的恰到好处，该模型 便能够取得高质量的结果，但我们很难解释清楚模型是如何做到这一点的；另外，在模型训练的不是那么恰好的情况下，我们又不知道到底是哪里出了问题。

尽管从基本面上去理解神经网络的工作原理是一件具有挑战性的事情，但是对于理解低维深度神经网络来说是一件相对容易的事情，这里低维是指神经网络模型中每一层仅有少量个数的神经元。事实上，我们可以通过创建可视化来彻底的理解 低维网络模型的行为和训练过程。并从这个角度，对神经网络的行为产生更深的直觉，并且发现神经网络和数学领域的拓扑之间的联系。

在此联系中，我们会发现许多有趣的事情，包括一个神经网络模型的复杂度至少需要达到怎样的下限值，才能实现对特定的数据集进行正确分类的能力。

一个简单的例子

我们从一个简单的数据集开始，该数据集是平面上的两条曲线数据。神经网络将对数据集中的点进行分类–即某个数据点属于两条曲线中的哪一条。

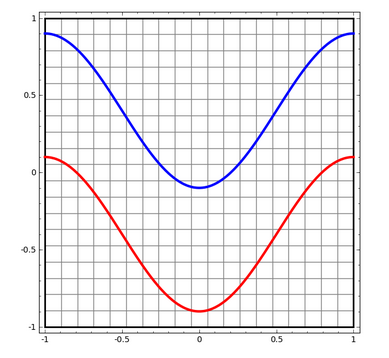
olah_two_curves

想要对神经网络模型或者其他算法模型的行为进行可视化，一种直接的方式便是去观测它对每一个可能的数据点是如何进行分类的。

为此，我们先以最简单的一类神经网络模型为例，该网络仅有一个输入层和一个输出层。该网络仅是简单的用一条直线对两类数据点进行区分 (代码参考jupyter notebook)。如下图所示

olah_two_curves_2

这类简单的神经网络并没有太大的用途。深度神经网络在输入/输出层之间通常具有多个隐藏层。下图是只有一个隐藏层的情况下的神经网络

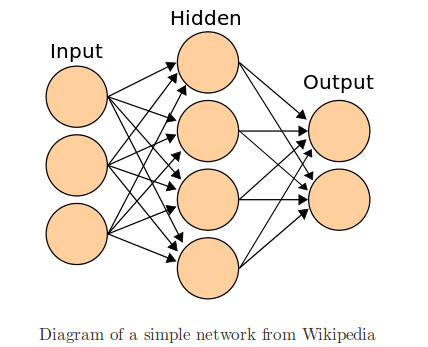
nn_one_hidden_layer

现在，上面的神经网络将如何对数据集进行分类呢？它是以一种更加复杂的曲线来对两类数据点进行分类

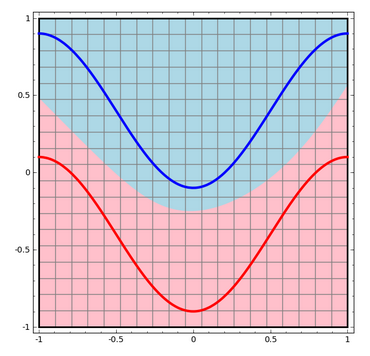
nn_one_hidden_layer_2

神经网络中的每一层将对输入的数据进行变换，生成新的特征表示(representation)。我们可以通过观察每一层的特征表示来查看网络是如何进行分类的。另外，当我们观测到最后一层特征表示的时候，我们将发现网络仅仅 使用一条线(在高维情形中则是一个超平面)对数据点进行分类。

在之前的可视化中，我们观察的是数据集的“原始”特征表示，这等同于观察输入层的数据。现在我们来观察数据经过第一次变换后的情况，也就是隐藏层的特征表示。

下图中的每一维对应于隐藏层中一个神经元的激活情况。

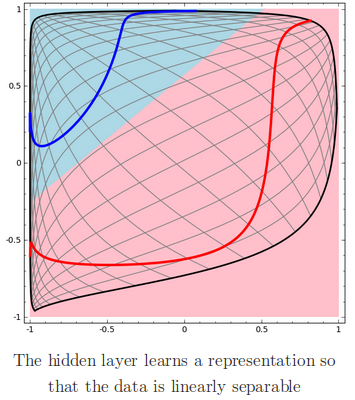
nn_one_hidden_layer_3

网络层的连续可视化

上一节中，我们通过观察每一层的特征表示来试着理解该网络模型。至此，我们得到了一个特征表示的列表(列表中每个特征表示对应一个网络层)。

然而更重要的是如何理解从一个特征表示（前一层）得到另一个特征表示（后一层）。幸好，神经网络层具有很好的属性，使得这个过程变得非常容易。

对于神经网络模型，可选的层有很多种类型，这里我们着重讨论 tanh 层。一个 层包括如下几步

  1. 通过权重矩阵 进行线性变换
  2. 通过向量 进行平移
  3. 逐点进行 函数变换

我们可以将其看做一种连续变换，如下图所示

其他类型的网络层所做的工作也类似，即仿射变换，及随后逐点应用单调激活函数。

我们通过上面的步骤来理解更为复杂的神经网络模型。比如，下面的网络将两条轻微交缠在一起的螺旋线进行分类，网络中使用了四个隐藏层。随着时间， 我们看到模型将“原始”数据变换到它所学习到的更高维度的特征表示，从而使得一开始纠缠在一起的螺旋线，在高维空间里变得线性可分。

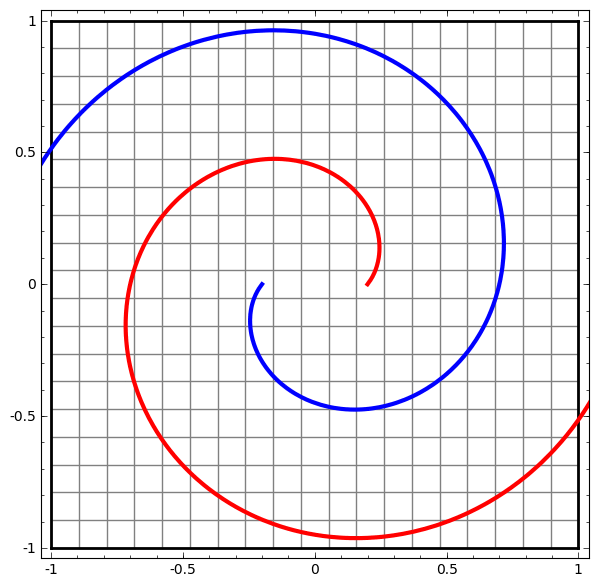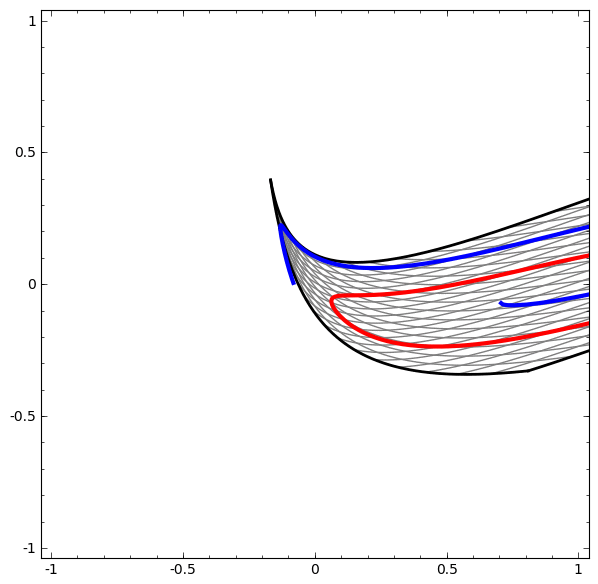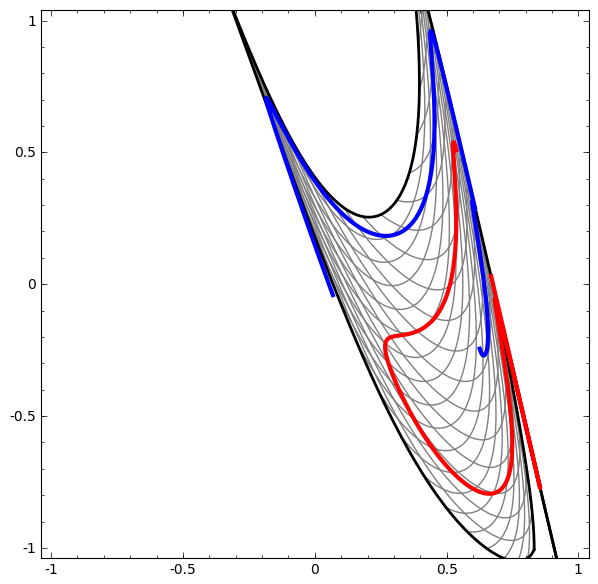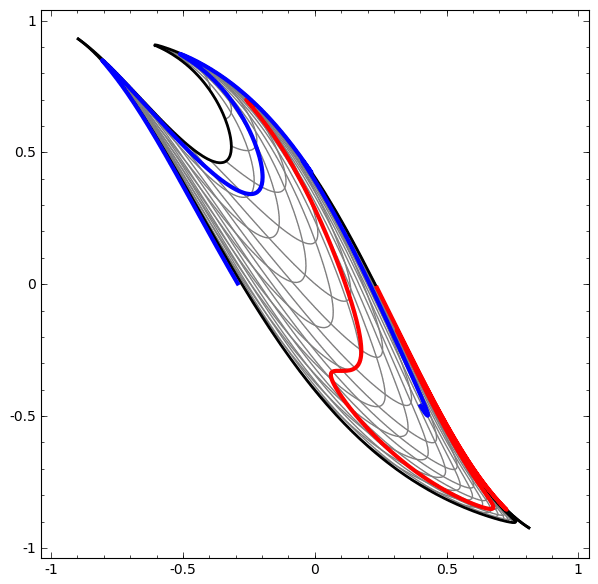
另一方面，下面的网络模型虽然也包含多个隐藏层，但并不能把两条纠缠更为紧密的螺旋线成功的分类。

这里需要点明的是上面的例子之所以看起来有难度，是因为我们使用了低维类型的神经网络模型。如果使用更宽(wider)的网络模型，也就是隐藏层中包含 更多的神经元，上面的问题解决起来就会很简单了。

tanh 层的拓扑

网络中的每一个层(layer) 都会对输入特征空间进行拉伸和压缩，但并不会对其进行切割、打破或者折叠。直觉上，我们可以认为层保持了特征数据的拓扑性质。 例如，某个集合的连接性并不会在经过层的处理后发生改变。

像上面这种不改变集合拓扑性质的转换操作被称作同胚 (homeomorphisms)。形式上，这种操作是双向连续函数的双射。

定理：如果权重矩阵 是非奇异的，那么对于输入/输出都是 维的层，它就是同胚的。

证明：

  1. 假设 具有非零行列式，那么操作 就是一个双射线性函数，并且具有线性的逆。已知线性函数具有连续性，因此此操作是同胚的。

  2. 平移操作，即 ，是同胚的。

  3. tanh （包括 sigmoid 和 softplus，但不包括 ReLU） 是连续函数，并且具有连续的逆函数。并且在我们所考虑的 领域和范围内他们是双射的。逐点进行函数变换也是同胚的。

因此，如果 具有非零的行列式，则 层操作就是同胚的。

上述定理对于任意叠加的层（保证每一层均是同胚的）操作同样适用。

现在考虑一个二维的数据集，该数据集的类标签为 和

其中红色代表 A，蓝色代表 B

结论：如果一个神经网络模型每一层神经元个数均小于 3，那么无论该模型深度是多少，都无法对上面的数据集进行正确分类。

如前面提到的，使用 sigmoid 或者 softmax 单元对数据集进行分类等价于在特征空间里寻找一个超平面（这里对应与一条直线）将 A, B 两个数据集 进行划分。如果隐藏层只有两个神经元，那么数据集的拓扑结构并没有改变，因此经过特征变换后仍然线性不可分，这与原始数据一样。

下面的动态图展示了随着这网络的不断训练，隐藏层的特征以及分类线的动态变化过程。可以看出分类线始终不能成功的对 A, B 进行正确分类。

Picture

最终，即使模型能够达到 80% 的分类正确率，但该模型并没有对数据集进行完全正确分类，仅仅是处于局部最优。

虽然上面的例子仅有一个隐藏层，但对于多个隐藏层的情况，只要每一层神经元个数 <= 2，结果不变。

论据：每一层要么是同胚操作，要么该层权重矩阵的行列式为0. 如果隐藏层是同胚操作，则 A 始终被 B 环绕，因此一条直线无法 做到将二者划分开。如果层的权重矩阵的行列式为0，此时数据集均坍缩到某一数轴上；并且由于隐藏层的操作为同胚，坍缩意味着 A 和 B 混合在该数轴上，因此仍然无法将二者划分开。

但是，当我们的隐藏层具有三个神经元节点时，上面无法划分的问题便可得到解决。这是因为模型训练后得到如下的特征：

Picture

此时，训练得到的特征可以轻松的被一超平面进行有效划分。

接下来，我们考虑一个更为简单的例子，一个一维的数据集：

Picture

A = [-1/3, 1/3]
B = [-1, -2/3] U [2/3, 1]

这里，隐藏层节点数目至少要达到两个才能对数据集进行正确分类。如下图所示，两个节点的隐藏层将数据点映射到了一条曲线上，从而使得 A 和 B 变得线性可分。上图中 x, y 坐标轴分别两个神经元节点，曲线上红色部分表示A数据集中的点经过隐藏层变换后的结果，蓝色部分 表示B数据集经过变换后的结果，最后使用一条直线就可以对两类数据集进行线性划分。

参考：

: