others

• 把 m个球放到n个箱子中，球不可分，箱子可分。每个箱子至少有一个球，共有

$$Y=C_{m-1}^{n-1}=\frac{(m-1)!}{(n-1)!(m-n)!} \qquad(Eq.1)$$

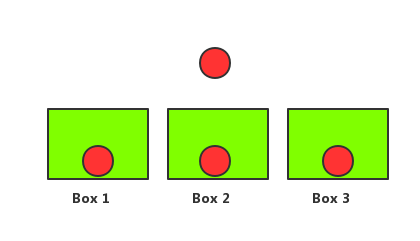
种分法。比如下图共有四个球(m=4), 三个箱子(n=3)，在保证每个箱子都有球的情况下共有 $Y=C_3^2=3$种放法。

• 现在有m个球，n个箱子($n\ge 2m-1$)。现将每个球放进某个箱子中(一个箱子至多放一个球)，在保证球互不紧邻的情况下共有多少种放法Y。如下图所示 m=2, n=4时，有Y=3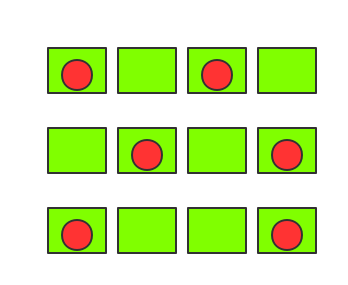

  

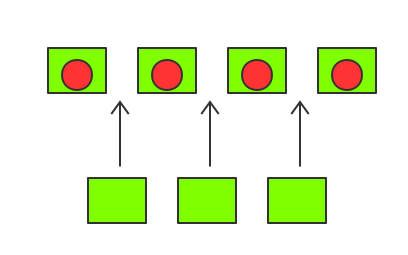
  • step 1： 将m个球放进盒子中后，剩余n-m空箱，为了保证已放球的箱子互相不紧邻，我们需要将剩余的n-m个空箱插入m个球之间的间隙(共有m-1个)，并保证每个间隙插入至少一个空箱，如下图所示

  

  • step2： step 1中的问题最终转化为将n-m个空箱划分为m-1个组(因此每个组中至少有一个空箱)，利用公式Eq.1，我们有$C_{n-m-1}^{m-1-1}$种划分方法。

  • step 3: 除了step 1和step 2中讨论的情况下，我们还有另外两种情况需要考虑，即考虑两侧(或单侧)有空箱的情况，如下图所示

  当两侧有空箱时,间隙个数为m+1；当单侧有空箱时，间隙个数为m

综上，$Y=C_{n-m-1}^{m-1-1}+2C_{n-m-1}^{m-1}+C_{n-m-1}^{m}$，其中等式右侧第一，二，三项分别表示序列两侧没有空箱，单侧有空箱，两侧有空箱的情况。

---

Random sampling

Consider the problem: after doing n times random sampling from n different balls with replacement, what is the probability of $p_i$ that we get $i$ different balls in our result (n balls).

If $i=1$, we have the number of different solutions $s_1 = C_n^1*\alpha_1 = C_n^1$,

where $\alpha_1=1$

if $i=2$, $s_2 = C_n^2 * \alpha_2 = C_n^2(2^n-C_2^1\alpha_1)$

if $i=3$, $s_3 = C_n^3 * \alpha_3 = C_n^3(3^n-C_3^2\alpha_2-C_3^1\alpha_1)$

…

if $i=i$, $s_i = C_n^i * \alpha_i = C_n^i (i^n -\sum_{j=1}^{j=i-1}C_i^j\alpha_j)$

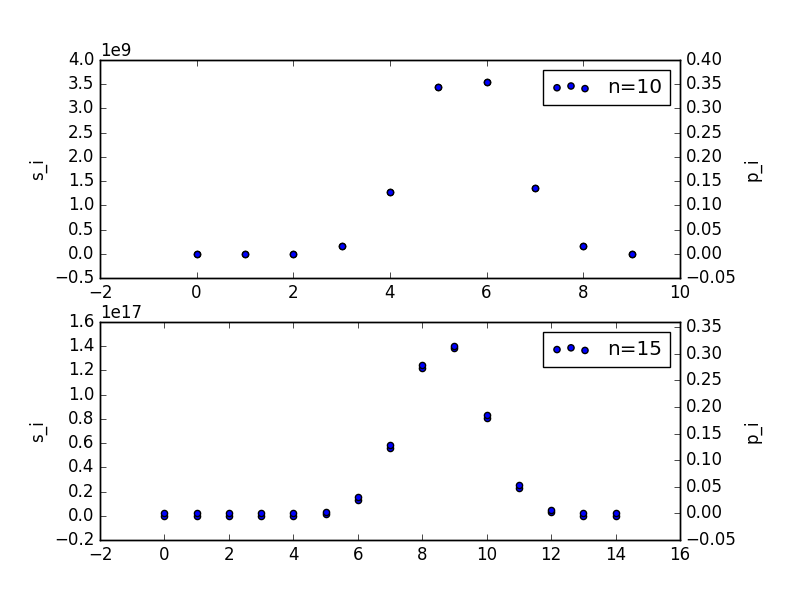
In the following, we show the scatter plots of $s_i$ and $p_i$ in cases $n=10$ and $n=15$, the code of computing $C_n^i$ and $\alpha_i$ can be found in github.

It worth noting that

$$\sum_{i=1}^n s_i = n^n$$

---

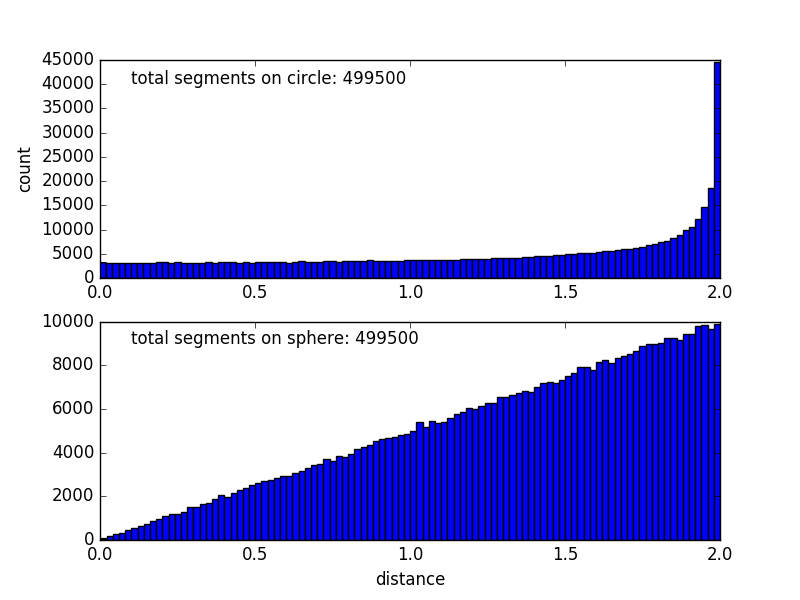
Distances distribution on circle/sphere

We compute the distribution of the distances of pairs of points on on a circle/sphere with radius $r = 1$, the data points are uniformly randomly sampled as the following code showing:

def circle_points(n_samples):
    """
    inputs
    ------
    n_samples: int

    return
    ------
    u: 2D np.ndarray with shape=[n_samples, 2]
    """
    theta = np.random.uniform(low=0.0, high=2 * np.pi, size=(n_samples, 1))
    u = np.concatenate([np.cos(theta), np.sin(theta)], axis=1)
    return u
  

def sphere_points(n_samples):
    """
    inputs
    ------
    n_samples: int

    return
    ------
    u: 2D np.ndarray with shape=[n_samples, 3]
    """
    theta = np.random.uniform(low=0.0, high=2 * np.pi, size=(n_samples, 1))
    z = np.random.uniform(low=-1.0, high=1.0, size=(n_samples, 1))
    x = np.sqrt(1 - z**2) * np.cos(theta)
    y = np.sqrt(1 - z**2) * np.sin(theta)

    u = np.concatenate([x, y, z], axis=1)
    return u

def distance(x, y):
    """
    inputs
    ------
    x: 2D np.ndarray with shape=[n1, dim]
    y: 2D np.ndarray with shape=[n2, dim]

    return
    ------
    dist: 2D np.ndarray with shape=[n1, n2], 
        dist[i, j] = distance(x[i], y[j])
    """
    assert len(x.shape) == len(y.shape) == 2
    assert x.shape[1] == y.shape[1]
    x = x[:, np.newaxis, :]
    y = y[np.newaxis, :, :]
    z = np.square(x - y)
    dist = np.sqrt(np.sum(z, axis=-1))
    return dist

Fig: distance distribution on circle (upper) / sphere (lower), 1000 data points are uniformly randomly sampled both on circle and sphere, and the total segments are 499500.