贝叶斯和最大似然

假如现在有一枚硬币，我们连续地抛出后，通过观测其正反面朝上的数据来估计任意抛出该硬币后，正面朝上的概率 $\mu$。这里假设连续抛出 $N$ 次， 正反面出现的情况为 $X=\{x_1, x_2, ..., x_N\}$， 其中 $x_i\in \{0, 1\}$ （$1$代表正面，$0$代表反面）。可以看出 $x$ 的分布满足

$$p(x|\mu) = \mu^x (1-\mu)^{1-x}$$

$\mu$ 称为此分布的参数。根据数据 $X$ 对参数 $\mu$ 进行的估计的方法有如下两种：

• 最大似然 方法
• 贝叶斯 方法

理解似然函数(likelihood function)

根据上面提到的硬币问题，如果存在 $\mu$（？），那么事件 $X$ 发生的概率为

$$p(X|\mu) = \prod_i p(x_i|\mu) = \prod_i \mu^{x_i}(1-\mu)^{1-x_i}$$

此概率函数称作似然函数(likelihood function)。最大似然方法认为如果存在 $\mu = \mu_0$ 能够使得似然函数取得最大值，那么 $\mu_0$ 便是我们要估计的参数值。因此我们将 $\mu$ 看做函数 $p(X|\mu)$ 的变量， 最大化 $p(X|\mu)$ 等价于最大化其对数：

$$ln \: p(X|\mu) = \sum_{n=1}^N \{x_n ln \mu + (1-x_n) ln (1 - \mu)\}$$

上式对 $\mu$ 求导，并使得导数值为0，便可得到 $\mu_0 = \frac{1}{N}\sum_{n=1}^Nx_n$。

根据上面的公式，如果我们连续扔了三次硬币，并且硬币全都正面朝上，那么可以得到 $\mu_0=1$。根据此结果，第四次扔硬币正面朝上的概率也为 $1$。 显然这样极端的结论并不一定成立，接下来介绍贝叶斯方法，该方法得出的结论将更加合理。

贝叶斯方法

贝叶斯公式如下

$$p(w|D)= \frac{p(D| w)p( w)}{p(D)}$$

其中 D: dataset, w: parameters

我们扔以抛硬币问题为例，则 $D$ 和 $w$ 分别表示观测数据 $X$ 和概率 $\mu$。贝叶斯方法的核心是先验假设，即我们假设概率值 $\mu$ 满足某种特定的分布， 比如 beta 分布：

$$beta(\mu|a, b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\:\mu^{a-1}(1-\mu)^{b-1} \qquad \mu \in (0, 1)$$

beta 分布满足 $\int_0^1 beta(\mu) d\mu = 1$，其中参数 a, b 可以看做本问题的超参数（决定参数 $\mu$ 的分布的参数）。 我们的目标是根据 $X$ 计算 $\mu$ 的分布函数，这不同于最大似然方法，该方法计算的是特定的参数值$\mu_0$。

根据贝叶斯公式我们有：

$$p(\mu|X) = \frac{p(X|\mu) p(\mu)}{p(X)} = c(a, b) \: \mu^{m+a-1}(1-\mu)^{l+b-1}$$

其中 c(a, b) 是分布函数的归一化系数，$m$ 和 $l$ 分别表示 $X$ 中 1, 0 （正反面）出现的次数。

上面的公式有什么意义呢？我们以 $a=2, b=2$ 初始化 beta 函数，则 $\mu$ 的先验分布如下图中的第一幅所示， $\mu=0.5$ 的概率值最大，也就是说在第一次扔硬币之前，硬币正面朝上和反面朝上的可能性都是一样的；而取其他值的概率相对较小，且分布曲线关于 $\mu=0.5$对称。 如果我们连续扔三次硬币，且每次硬币均正面朝上，那么根据上面的公式计算出的后验概率分别对应于下图中的第二、三、四幅图。

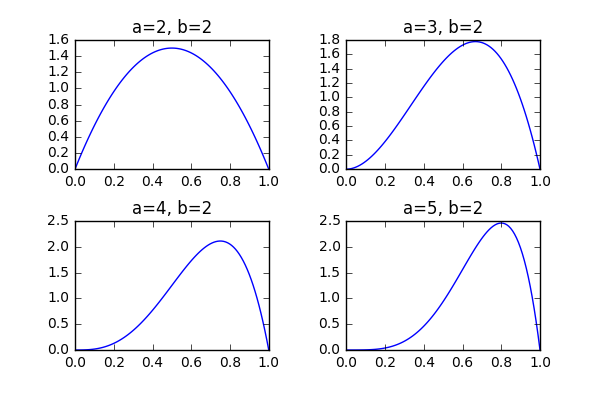
可以看出第一次扔硬币出现正面朝上，使得

$$beta(\mu|2, 2) + x_1 \longrightarrow beta(\mu|3, 2)$$

该后验概率使得 $\mu$ 的分布向右偏置，也就是正面朝上的概率大于反面朝上的概率。 第二次扔硬币再次出现正面朝上，使得

$$beta(\mu|3, 2) + x_2 \longrightarrow beta(\mu|4, 2)$$

后验概率分布继续向右偏置， 第三次扔硬币再次出现正面朝上，使得

$$beta(\mu|4, 2) + x_3 \longrightarrow beta(\mu|5, 2)$$

因此，随着新的结果不断出现，贝叶斯公式可以不断的调整参数分布曲线的形状，以更好的反映所观测到的数据集 $X$。

推理 (inference)

根据上面介绍的两种方法得出关于参数 $\mu$ 的估计后，我们最后的目的是进行推理，也就是计算出下次抛硬币出现正面(反面)朝上的概率值 $p_1$ ($p_0$)。

根据最大似然方法，我们有：

$$p_1 = \mu, \quad p_0 = 1- p_1$$

根据贝叶斯方法，我们有：

$$p_1 = \int_0^1 \mu \cdot p(\mu|X) d\mu \quad p_0 = 1- p_1$$

可以看出当所有观测值均为正面朝上时，贝叶斯方法得出的结果会使得 $p_1$无限趋于 1 （$p_1 \rightarrow 1$），但并不会出现最大似然方法所得出的极端结果 $p_1=1$。

曲线拟合问题

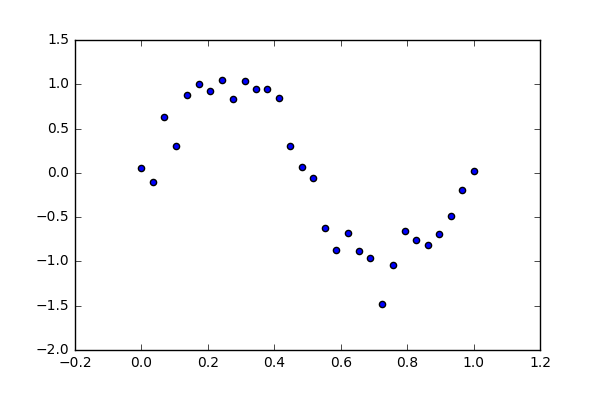
如图所示，现在有观测数据集 $(X, t) = \{(x_1, t_1), (x_2, t_2), .., (x_N, t_N)\}$， 我们期望寻找参数 $\vec w$ （$\vec w$ 称为权重） 对该数据集进行多项式拟合：

$$y = w_0 + w_1x + w_2 x^2 + ... + w_M x^M$$

对于这种简单的问题，通过最小化平方和误差来计算相应的权重值是一种常用的办法，即最小化：

$$E(\vec w) = \frac{1}{2}\sum_{n=1}^N (y_n - t_n)^2$$

其中 $y_n = y(x_n, \vec w)$，这种办法有唯一解，这是因为选取的 $E(\vec w)$ 是二次的。

现在我们通过最大似然方法和贝叶斯方法对参数 $\vec w$ 进行估计。

• 最大似然

对于抛硬币问题，我们假设每次出现的结果满足 $p(x|\mu) = \mu^x (1-\mu)^{1-x}$；在这里，对于特定的输入值 $x$ 和参数 $\vec w$，假设相应的目标值 $t$ 满足高斯分布：

$$p(t|x, \vec w, \sigma_1) = N(t|\mu, \sigma_1)$$

这种假设实际上表达了目标变量 $t$ 的不确定性；上式中均值 $\mu$ 取作 $\mu = y(x, \vec w)$。

最大似然的方法是通过最小化似然函数来确定参数 $\vec w$ 和 $\sigma_1$ 的值，此时，似然函数为

$$p(t|X, \vec w, \sigma_1) = \prod_{n=1}^N N(t_n|y(x_n, \vec w), \sigma_1)$$

对上式取对数可得

$$ln\: p(t|X, \vec w, \sigma_1) = -\frac{1}{2\sigma_1}\sum_{n=1}^N (y_n - t_n)^2 + \frac{N}{2}ln\:\frac{1}{\sigma_1} -\frac{N}{2}ln\: 2\pi$$

观测上面的式子，可以看出通过最小化平方和误差

$$\sum_{n=1}^N (y_n - t_n)^2 \quad y_n = y(x_n, \vec w)$$

得到的权重 $w$ 便是所要求的解；同时，对 $\sigma_1$ 求偏导，可以得出对应的解为

$$\sigma_1 = \frac{1}{N} \sum_{n=1}^N (y_n - t_n)^2$$

这样，当我们有新的输入值 $x_k$时，便可以使用计算得到的权重 $\vec w$ 和方差 $\sigma^2$ 对目标值 $t_k$ 进行预测，预测结果为

$$p(t_k| x_k, \vec w, \sigma_1) = N(t| \mu=y(x_k, w), \sigma_1)$$

• 贝叶斯方法

现在我们需要引入参数 $\vec w$ 的先验概率，简单起见，假设该先验概率满足高斯分布

$$p(\vec w|\sigma_2) = N(\vec w|\vec 0, \sigma_2 I) = (\frac{1}{2\pi\sigma_2})^{\frac{M+1}{2}}exp\{-\frac{1}{2\sigma_2}\vec w^T\vec w\}$$

使用贝叶斯公式，有

$$p(\vec w|X, t, \sigma_1, \sigma_2) \propto p(t| X, \vec w, \sigma_1) \cdot p(\vec w| \sigma_2)$$

现在，在我们已知数据集 $(X, t)$ 的条件下，上面的式子便是参数 $\vec w$ 所满足的概率分布函数 （即后验概率，其中 $\sigma_1$ 和 $\sigma_2$ 称为超参数， 在训练模型之前可以通过经验确定他们的值）

当我们有新的输入值 $x_k$ 时，可以通过对后验概率函数进行积分的步骤求出目标值 $t_k$ 所满足的分布

$$p(t_k|x_k, \vec w, \sigma_1, \sigma_2) = \int p(t_k|x_k, \vec w, \sigma_1) \cdot p(\vec w| X, t, \sigma_2)$$

在实际应用过程中，我们很少能够得到后验概率的解析表达式，这时也就不能得到上面的积分表达式；解决的办法便是通过最大化后验概率，近似的解出权重 $w$ 的值， 以此对目标值$t_k$ 进行概率预测。最大化上面的后验概率，便是最小化下面的公式

$$\frac{1}{2\sigma_1}\sum_{n=1}^N (y_n - t_n)^2 + \frac{1}{2\sigma_2}\vec w^T \vec w$$

总结

上面介绍了最大似然方法和贝叶斯方法估计模型参数的例子，两种方法中都需要对所解决的问题进行必要的统计分布假设：

• 抛硬币问题中，假设每次的结果满足 $p(x|\mu) = \mu^x (1-\mu)^{1-x}$，

• 曲线拟合问题中，假设预测值满足 $p(t|x, \vec w, \sigma_1) = N(t|\mu, \sigma_1)$。

而两种方法不同的地方在于：

最大似然方法中，根据统计假设得到的是 数据集 关于 参数 的条件分布函数 $p(X, t | \vec w)$， 这里求得的是关于参数 $\vec w$ 的点估计。

贝叶斯方法中，除了必要的统计分布假设外，还需要进一步对参数 $\vec w$ 的分布进行先验假设，进而根据贝叶斯公式计算 参数 关于 数据集 的条件概率分布函数 $p(\vec w| X, t)$， 这里得到的是关于参数 $\vec w$ 的概率密度估计。